1.虚拟机(Virtual Machine,VM)与容器的区别
VM 和容器都是用于为应用程序和服务提供独立且可移植的计算环境的虚拟化技术:
- VM 模拟整个计算机,包括虚拟化硬件、OS、用户模式及其自身的内核模式。 VM 非常灵活,可为应用程序提供广泛的支持;但是,VM 往往比较大,会消耗主机资源。
- 容器(如前所述)基于主机操作系统内核构建,并包含打包的应用的独立用户模式进程。 这有助于使容器轻量化且快速启动。
2. VM与容器相似性和差异性
下表总结了 VM 和容器的功能之间的相似之处和不同之处。
| 功能 | VM | 容器 |
|---|---|---|
| 隔离 | 提供与主机 OS 和其他 VM 的完全隔离 | 提供与主机和其他容器的轻型隔离。 |
| (OS) | 运行完整的 OS,包括内核 | 仅运行 OS 的用户模式部分 |
| 来宾兼容性 | 能够在 VM 内运行任何受支持的 OS | 如果在进程隔离模式下运行,则必须在与主机类型相同的内核 (OS) 上运行;在 Windows 主机上运行非 Windows 容器时,Hyper-V 隔离模式提供更大的灵活性 |
| 部署 | 使用 Hyper-V 管理器或其他 VM 管理工具进行部署 | 使用 Docker 进行部署和管理,可以使用 Kubernetes 等业务流程协调程序部署多个容器 |
| 持久存储 | 使用虚拟硬盘文件或服务器消息块 (SMB) 共享 | 当容器不再存在时,数据不会持久保存。 若要使用 Windows Server 保存容器中的数据,需要使用绑定装载或命名卷 |
| 负载均衡 | 按需使用 Windows 故障转移群集移动 VM | 使用业务流程协调程序自动启动和停止容器 |
| 网络 | 使用虚拟网络适配器 | 创建默认 NAT 网络,该网络使用内部虚拟交换机 (vSwitch) 和名为 WinNAT 的 Windows 组件 |
通常在高度优化的 VM 中预配容器,以提供增强的隔离和安全性。
3. 容器的优点
概括而言,容器具有以下优点:
- 需要相对较少的资源。 与 VM 相比,它们消耗的资源更少。
- 快速启动。 容器启动时间大致相当于启动新进程所需的时间。
- 提高服务器密度。 与 VM 相比,容器可以更高效地利用可用硬件的内存、磁盘和 CPU。 这使得空闲服务器减少,从而更好地利用现有的计算资源。 这对于云提供商和用户尤为重要,因为这样可以降低成本。
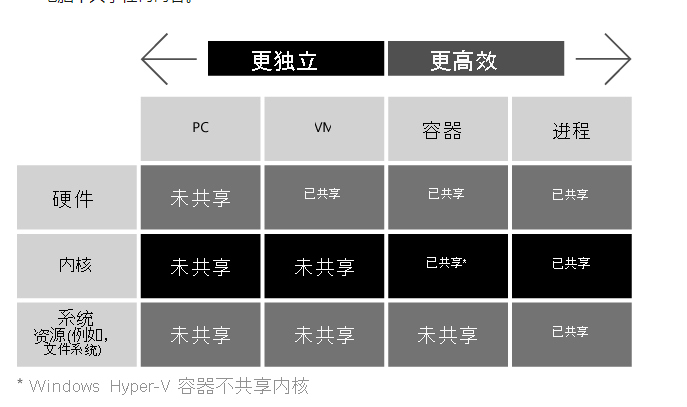
下图提供了电脑、VM、容器和进程之间的隔离和效率的比较:
- 电脑提供最大程度的隔离。 VM、容器和进程的隔离性递减。
- 进程提供的效率最高,进而可能密度最大。 容器、VM 和电脑的效率递减。
- 内核和系统资源(如文件系统)均可共享:
- 仅共享硬件
- 容器共享硬件和内核(Windows Hyper-V 容器除外,它不共享内核)
- 进程共享硬件、内核和系统资源
- 电脑不共享任何内容
对于永久性存储,可以使用绑定装载在本地计算机上装载一个位置。 重启容器时或要与多个容器共享文件时,该位置中的文件将可供使用。 如果希望容器在多台计算机上运行,并且该容器有权访问相同的文件,则应改用命名卷或 SMB 装载。
请勿将敏感目录(如 C:\)绑定装载到不受信任的容器中。 这会允许不受信任的容器更改它通常无法访问的主机上的文件,并且可能会产生安全漏洞。
4. VM和容器的选择
4.1 何时选择 VM
在以下情况使用 VM:
- 需要管理多个操作系统。
- 需要运行应用,该应用需要完整 OS 的所有资源和服务,如图形用户界面 (GUI)。
- 需要一个可持久保存更改的环境。
- 需要完全隔离性和安全性。
4.2 何时选择容器
在以下情况使用容器:
- 需要快速启动的轻型应用程序包。
- 需要部署单个应用的多个实例。
- 需要按需运行非持久的应用或进程。
- 需要部署可在任何底层基础结构上运行的应用。
5. Windows系统容器的隔离模式
Docker容器最初只能在Linux和MacOS系统下运行,在Windows系统下运行并不稳定。但在新的Windows10专业版与Windows Server 2019上,对Docker的支持已经优化了很多,可以应用于生产场景。在Windows Server下,可以通过Windows Server进程隔离和Hyper-V隔离两种模式运行Docker容器。这两种隔离模式也是WSL(Windows Subsystem for Linux)一代和二代默认的两种模式。
5.1 Windows Server 容器的进程隔离模式
作为 Windows Server 容器的传统隔离模式,进程隔离模式允许多个容器实例在主机上同时运行。 在此模式下运行时,容器与容器之间以及容器与主机 OS 之间会共享同一个内核。 每个预配的容器都具有自己的用户模式,允许 Windows 和应用进程独立于其他容器运行。 将 Windows 容器配置为使用进程隔离模式时,容器可以在同一台计算机上以隔离状态运行多个应用,但它们不提供安全性增强的隔离。
Docker 是开源工具、解决方案和基于云的服务的集合,它们提供了一种通用模型,用于将应用代码打包(也称为容器化)为软件开发的标准化单元。
启动新容器时,Docker 会与计算服务进行通信,以基于映像创建新容器。 对于每个容器,Docker 都会创建一个 Windows 容器。 每个 Windows 容器都需要一组系统进程,这些进程在每个容器中始终相同。 然后,可以使用自己的应用程序进程来区分每个容器。 为此,可以使用 Microsoft Internet Information Services (IIS) 或在容器中运行的 SQL Server 进程。
5.2 Hyper-V 容器的 Hyper-V 隔离模式
当容器共享内核和内存时,如果 Windows OS 中出现漏洞,应用程序可能会摆脱其沙盒环境,并意外执行恶意操作。 为避免出现这种情况,Windows 提供了另一种更安全的运行容器的方法,称为 Hyper-V 隔离模式,有时也称为 Hyper-V 容器。
在 Hyper-V 隔离模式下,每个容器都在高度优化的 VM 中运行。 Hyper-V 隔离模式的优点是,每个容器实际上都有自己的内核,这提供了增强级别的稳定性和安全性。 VM 在每个容器和主机之间提供附加的硬件级隔离层。 部署时,使用 Hyper-V 隔离模式的容器会在数秒内启动,这比使用完整 Windows OS 的 VM 要快得多。
在 Windows Server 上运行的基于 Windows 的容器默认使用进程隔离模式。 在 Windows 10 专业版和企业版上运行的基于 Windows 的容器默认使用 Hyper-V 隔离模式。
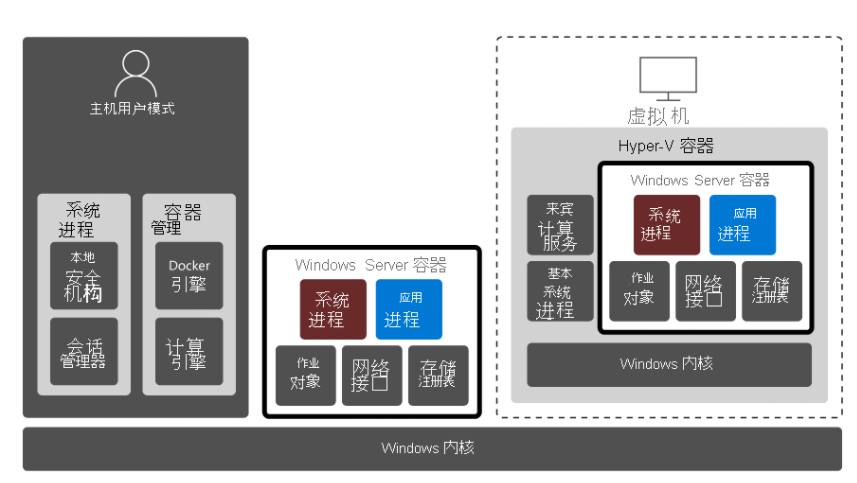
下图对 Windows Server 和 Hyper-V 容器的体系结构及其两种隔离模式进行了比较。 此图说明主机 Windows 内核由主机用户模式和 Windows Server 共享。 在该共享内核上运行的是一个虚拟机,该虚拟机中有一个 Hyper-V 容器。 Hyper-V 容器具有自己的 Windows 内核,该内核不共享。
Windows 10 中的进程隔离模式仅用于开发和测试。 从 Windows 10 2018 年 10 月更新开始,运行 Windows 10 专业版或企业版主机的用户可以在进程隔离模式下运行 Windows 容器。 用户必须使用 –isolation=process 参数来直接请求进程隔离模式。 你的主机必须运行 Windows 10 内部版本 17763+,并且你必须有包含引擎 18.09 或更高版本的 Docker 版本
由于 Windows Server 容器和主机操作系统共享内核,因此必须确保主机与容器映像版本标记匹配,否则容器可能无法启动或显示未定义的行为。
5.3 使用 Docker 命令指定隔离模式
使用 Docker 创建容器时,可以使用 –isolation 参数来指定隔离模式(进程隔离模式或 Hyper-V 隔离模式均可),使用以下命令选择进程隔离或hyperv隔离模式创建容器:
docker run -it --isolation=process mcr.microsoft.com/windows/servercore:ltsc2019 cmd
docker run -it --isolation=hyperv mcr.microsoft.com/windows/servercore:ltsc2019 cmd`